How to Read Latitude, Sun Angle, Daylength and Seasonality Through Insolation Charts

Right Triangle Side and Angle Calculator

Created by Hanna Pamuła , PhD candidate

Concluding updated:

Nov 12, 2021

Table of contents:

• How to find the sides of a right triangle
• How to find the angle of a right triangle
• How do you lot solve a right angle triangle with only one side?
• How to find the missing side of a right triangle? How to discover the angle? Example
• FAQ

Finding out the missing side or angle couldn't be easier than with our great tool - correct triangle side and angle calculator. Cull two given values, type them into the reckoner and the remaining unknowns will be determined in a blink of an centre! If you are wondering how to find the missing side of a right triangle, go on scrolling and yous'll find the formulas behind our calculator.

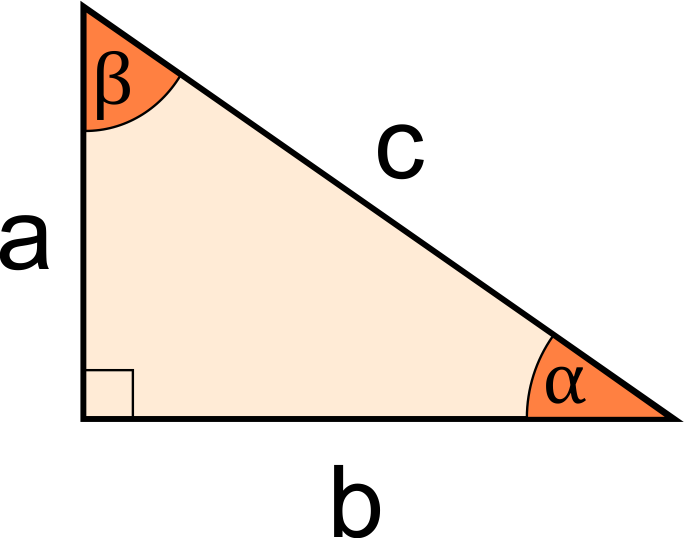
How to find the sides of a right triangle

In that location are a few methods of obtaining correct triangle side lengths. Depending on what is given, you can use dissimilar relationships or laws to discover the missing side:

1. Given two sides

If yous know two other sides of the right triangle, information technology's the easiest choice; all you need to do is apply the Pythagorean theorem:

a² + b² = c²

• if leg a is the missing side, and so transform the equation to the class when a is on 1 side, and accept a square root:

  a = √(c² - b²)

• if leg b is unknown, then

  b = √(c² - a²)

• for hypotenuse c missing, the formula is

  c = √(a² + b²)

2. Given angle and hypotenuse

Utilize the law of sines or trigonometry to find the right triangle side lengths:

• a = c * sin(α) or a = c * cos(β)

• b = c * sin(β) or b = c * cos(α)

3. Given angle and one leg

Notice the missing leg using trigonometric functions:

• a = b * tan(α)

• b = a * tan(β)

4. Given area and one leg

Equally we remember from bones triangle area formula, we tin can summate the expanse past multiplying triangle top and base and dividing the result by two. A correct triangle is a special case of a scalene triangle, in which one leg is the height when the second leg is the base of operations, so the equation gets simplified to:

surface area = a * b / 2

For example, if we know only the right triangle area and the length of the leg a, we can derive the equation for other sides:

• b = 2 * area / a
• c = √(a² + (ii * area / a)²)

How to detect the angle of a correct triangle

If yous know ane angle apart from the right angle, adding of the 3rd 1 is a piece of block:

Given β: α = 90 - β

Given α: β = 90 - α

However, if only two sides of a triangle are given, finding the angles of a right triangle requires applying some basic trigonometric functions:

for α

• sin(α) = a / c so α = arcsin(a / c) (inverse sine)
• cos(α) = b / c and then α = arccos(b / c) (inverse cosine)
• tan(α) = a / b so α = arctan(a / b) (inverse tangent)
• cot(α) = b / a so α = arccot(b / a) (inverse cotangent)

and for β

• sin(β) = b / c then β = arcsin(b / c) (inverse sine)
• cos(β) = a / c so β = arccos(a / c) (inverse cosine)
• tan(β) = b / a and then β = arctan(b / a) (inverse tangent)
• cot(β) = a / b and then β = arccot(a / b) (inverse cotangent)

How do you solve a right angle triangle with only ane side?

To solve a triangle with one side, you too need one of the not-correct angled angles. If not, information technology is impossible:

1. If you lot take the hypotenuse, multiply information technology by sin(θ) to get the length of the side reverse to the angle.
2. Alternatively, multiply the hypotenuse by cos(θ) to get the side next to the angle.
3. If you have the not-hypotenuse side adjacent to the bending, split up it by cos(θ) to get the length of the hypotenuse.
4. Alternatively, multiply this length by tan(θ) to become the length of the side opposite to the angle.
5. If you take an angle and the side contrary to it, you lot tin can separate the side length by sin(θ) to go the hypotenuse.
6. Alternatively, split up the length by tan(θ) to get the length of the side next to the angle.

How to find the missing side of a correct triangle? How to find the angle? Example

Let's bear witness how to discover the sides of a correct triangle with this tool:

1. Assume we want to find the missing side given surface area and one side. Select the proper option from a driblet-downward listing. It's the third one.
2. Type in the given values. For example, an expanse of a correct triangle is equal to 28 in² and b = 9 in.
3. Our right triangle side and angle figurer displays missing sides and angles! Now we know that:

• a = half dozen.222 in
• c = 10.941 in
• α = 34.66°
• β = 55.34°

Now, let'due south check how does finding angles of a right triangle work:

1. Refresh the computer. Pick the selection you need. Assume that we have two sides and we want to notice all angles. The default option is the right one.
2. Enter the side lengths. Our right triangle has a hypotenuse equal to 13 in and a leg a = 5 in.
3. Missing side and angles announced. In our instance, b = 12 in, α = 67.38° and β = 22.62°.

FAQ

How many lines of symmetry does a correct triangle have?

If a right triangle is isosceles (i.e., its two non-hypotenuse sides are the same length) it has one line of symmetry. Otherwise, the triangle will have no lines of symmetry.

Tin a right angled triangle take equal sides?

No, a right triangle cannot have all 3 sides equal, every bit all iii angles cannot besides exist equal, as one has to exist 90° by definition. A correct triangle tin, yet, accept its two non-hypotenuse sides be equal in length. This would also mean the two other angles are equal to 45°.

Are all right triangles similar?

Not all right angled triangles are similar, although some can be. They are similar if all their angles are the same length, or if the ratio of 2 of their sides is the aforementioned.

Hanna Pamuła , PhD candidate

escototheriest.blogspot.com

Source: https://www.omnicalculator.com/math/right-triangle-side-angle

Share this post